推倒万亿参数大模型内存墙,万字长文:从第一性原理看神经网络量化
【新智元导读】
为了应对大模型不断复杂的推理和训练,英伟达、AMD、英特尔、谷歌、微软、Meta、Arm、高通、MatX以及Lemurian Labs,纷纷开始研发全新的硬件解决方案。
从32位,到16位,再到8位,量化在加速神经⽹络⽅⾯发挥了巨⼤作⽤。
放眼一看,世界把所有的⽬光都聚焦在数字格式上。因为在过去的⼗年中,AI硬件效率的提⾼有很⼤⼀部分要归功于数字格式。
较低精度的数字格式,帮助推倒了数十亿参数模型的内存墙。
英伟达声称,过去10年,单芯⽚TOPS提升了足足1000倍,英伟达自身就加起来达16倍。相⽐之下,从28nm到5nm,⼯艺技术的改进仅为2.5倍!
Semianalysis的最新文章中,从数字格式的基本原理出发,深⼊探讨了神经⽹络量化的技术现状。
本⽂中,将介绍浮点与整数、电路设计注意事项、块浮点、MSFP、微缩格式、对数系统等内容,还会介绍量化和推理数字格式的差异,以及⾼精度与低精度训练方法。
此外,鉴于量化和精度损失带来的挑战,稳重还将讨论模型的下⼀步发展。
最后,文中将介绍英伟达、AMD、英特尔、谷歌、微软、Meta、Arm、高通、 MatX和Lemurian Labs等硬件开发商在扩展⽬前流⾏的8位格式(如FP8和Int8) 时将采⽤的技术。
矩阵乘法
任何现代机器学习模型的主体都是矩阵乘法。
在GPT-3中,每⼀层都要进⾏⼤量的矩阵乘法运算:例如,其中⼀个具体运算是⼀个(2048 x 12288)矩阵乘以⼀个(12288 x 49152)矩阵,然后输出⼀个(2048 x 49152)矩阵。
重要的是如何计算输出矩阵中的每个元素,这可以归结为两个⾮常⼤的向量的点积(在上⾯的例⼦中,⼤⼩为12288)。
这包括12288次乘法和12277次加法,累积成⼀个数字,即输出矩阵的单个元素。
通常情况下,通过硬件将累加器寄存器初始化为0,然后反复:
- 乘以 x_i * w_i
- 将其加⼊累加器
每个周期的吞吐量均为1,经过~12288个周期后,输出矩阵的单个元素的累加完成。
这种「融合乘加」运算(FMA)是机器学习的基本计算单元:芯⽚上成千上万个FMA单元经过策略性排列,可⾼效地重复使⽤数据,从⽽并⾏计算输出矩阵的许多元素,从而减少所需的周期数。
上图中的所有数字都需要以某种⽅式,在芯⽚内的某个位置⽤位表示:
- x_i,输⼊激活
- w_i,权重
- p_i,成对乘积
- 在整个输出完成累积之前,所有中间部分累积加和
- 最终输出总和
在这个巨⼤的设计空间中,⽬前⼤多数机器学习量化研究都归结为两个⽬标:
1. 实现良好的能量和⾯积效率。这主要取决于权重和激活所使⽤的数字格式。
2. 既要⾜够精确地存储数千亿个权重,又要使⽤尽可能少的位,以便从容量和带宽的角度减少内存占⽤。这取决于⽤于存储权重的数字格式。
这些⽬标有时是⼀致的,有时是相悖的。接下来文章将对两者进⾏深⼊探讨。
数字格式设计目标1:芯片效率
许多机器学习芯⽚计算性能的根本限制在于功耗。
虽然H100在论文中可以实现2,000 TFLOPS的计算能⼒,但在此之前就会遇到功耗限制,因此每焦⽿能量的FLOPs是⼀个极其重要的跟踪指标。
鉴于现在的训练运⾏经常超过1e25 FLOP,我们需要极其⾼效的芯⽚,在数⽉内消耗兆⽡级的电⼒,以击败SOTA。
基本数字格式
首先深入了解计算中最基本的数字格式:整数。
基数为2正整数
正整数可以用2进制(基数为2)来自然表示。这种表示法称为UINT,即⽆符号整数。下⾯是⼀些8位⽆符号整数的例⼦,也称为UINT8,从0到255。
这些整数的位数不限,但通常只⽀持以下四种格式:UINT8、UINT16、UINT32和UINT64。
负整数
负整数需要⼀个符号来区分正负,只需在最显著位加上⼀个符号即可:例如, 0011表示+3,1011表示-3。这称为符号-数值表示。
下⾯是INT8的⼀些示例,INT8从-128到127。请注意,由于第⼀位是符号,最⼤值实际上减半了,从255到127。
符号大小是直观的,但效率很低——你的电路必须实现相当不同的加法和减法算法,⽽这些算法又与⽆符号整数的电路不同。
有趣的是,硬件设计⼈员可以通过使⽤⼆进制表示法来解决这个问题,这样就可以对正数、负数和⽆符号数使⽤完全相同的进位阶梯电路。所有现代CPU都使⽤⼆进制表⽰法。
在⽆符号int8中,255的最⼤值是1111111111。在有符号int8中,最⼩值为-128,最⼤值为127。
为了让INT8和UINT8共享硬件资源,可以⽤1111111111来表⽰-1。现在,当数字1相加时,会溢出到00000000,如预期的那样表示0。同样,11111110也可以表⽰为-2。
溢出是一种特征!实际上,0到127被映射为正常值,128到255被直接映射到-128到-1。
定点数
更进⼀步说,我们可以在现有硬件上轻松制作新的数字格式,⽆需修改。
虽然这些都是整数,但你也可以想象它们是其他数的倍数!例如,0.025就是千分之25,可以直接存储为整数25。现在,我们只需在其他地⽅记住所有正在使⽤的数字都是千分之⼀。
新的「数字格式」可以⽤千分之⼀来表示-0.128到0.127的数字,实际逻辑没有变化。整数仍被视为整数,然后⼩数点被固定在右起第三个位置。这种策略称为定点法。
⼀般来说,这是⼀个有⽤的策略,本⽂中会经常提到——如果你想改变可以表示的数字范围,可以在某个地⽅添加⼀个⽐例因⼦。(很明显,你可以在⼆进制中这样做,但⼗进制更容易讨论)。
浮点数
不过,定点也有⼀些缺点,尤其是乘法运算。⽐⽅说,你需要计算1万亿乘以1万亿分之⼀。
⼤⼩上的巨⼤差异就是⾼「动态范围」的⼀个例⼦。那么10^12和10^-12都必须⽤数字格式来表示,因此很容易计算出需要多少位:从0到1万亿,以1万亿为增量,需要10^24的增量,log2(10^24)~= 80 位,才能以我们想要的精度表示动态范围。
每个数字是80位显然是非常浪费的。你不⼀定关⼼绝对精度,你需要关⼼的是相对精度。
因此,即使上述格式能够准确区分1万亿和999,999,999,999.9999999999之间的误差(⼀般也不需要区分)。⼤多数情况下,你关⼼的是相对于数字⼤⼩的误差量。
这正是科学记数法所要解决的问题:在前⾯的例⼦中,我们可以将⼀万亿写成1.00 * 10^12,将⼀万亿分之⼀写成 1.00 * 10^-12,这样存储量就⼩得多了。
这样虽然更复杂,但可以让你在相同的上下⽂中毫⽆顾虑地表示极⼤和极⼩的数字。
因此,除了符号和数值外,我们现在还有⼀个指数。IEEE 754-1985在当时使⽤的许多略有不同的⼆进制格式中,标准化了业界通⽤的⼆进制存储⽅式。
主要的有趣格式——32位浮点数(float32或FP32)可以描述为 (1,8,23):1个符号位、8个指数位和23个尾数位。
- 符号位为0表⽰正,1表示为负。
- 指数位被解释为⽆符号整数e,代表⽐例因⼦2^e-127,其价值介于2^-126和2^127。更多的指数位意味着更⼤的动态范围。
- 尾数位代表数值1。更多的尾数位意味着更⾼的相对精度。
其他位宽已被标准化或显示采⽤,例如FP16(1,5,10)和BF16(1,8,7)。而争论的焦点在于范围与精度。
FP8(1,5,2或1,4,3)最近在OCP标准中标准化了一些额外的奇怪规定,但目前还没有定论。许多人工智能硬件公司已经实现了具有稍微优越的变体的芯片,但这些变体与标准不兼容。
芯片效率
说回硬件效率,所使⽤的数字格式对所需的芯⽚⾯积和功耗有巨⼤影响。
整数芯片电路设计
整数加法器是有史以来研究得最透彻的芯片设计问题。
虽然加法器的实际实现要复杂得多,但有⼀种⽅法可以让我们把加法器想象成⼀路加法并根据需要携带1,因此从某种意义上说,⼀个n位加法器所做的⼯作量与n成正⽐。
关于乘法,回想⼀下⼩学的长乘法。我们进⾏n位数乘以1位数的乘积,最后将所有结果相加。
在⼆进制中,乘以⼀位数是微不⾜道的(0或1)。这意味着n位乘法器实质上是n位加法器的n次重复,因此⼯作量与n^2成正⽐。
虽然实际应⽤因⾯积、功耗和频率限制⽽⼤不相同,但⼀般来说:1)乘法器⽐加法器昂贵得多;2)在低位数(8位及以下)情况下,FMA的功耗和⾯积成本相对于加法器的贡献越来越⼤(n对n^2缩放)。
浮点电路
浮点运算单位则⼤不相同。相⽐之下,乘积/乘法相对简单。
- 如果输⼊的符号中正好有⼀个是负号,则符号为负,否则为正。
- 指数是输⼊指数的整数和。
- 尾数是输⼊尾数的整数乘积。
相⽐之下,总和相当复杂。
- ⾸先,求指数的差值。(假设exp1⾄少和exp2⼀样⼤,如果不⼀样⼤,则在指令中进⾏交换)
- 将尾数2向下移动(exp1-exp2),使其与尾数1对齐。
- 在每个尾数中加⼊⼀个隐含的前导1。如果⼀个符号是负数,则对其中⼀个尾数进⾏2的补码运算。
- 将尾数相加形成输出尾数。
- 如果出现溢出,则将结果指数增加1,并将尾数向下移动。
- 如果结果为负数,则将其转换回⽆符号尾数,并将输出符号设为负数。
- 对尾数进⾏归⼀化处理,使其具有前导1,然后删去隐式前导1。
- 对尾数进⾏适当的四舍五⼊(通常是四舍五⼊到最近的偶数)。
值得注意的是,浮点乘法甚⾄可以⽐整数乘法成本更少,因为尾数乘积中的位数更少,⽽指数的加法器⽐乘法器⼩得多,⼏乎没有关系。
显然,这也是经过极度简化的,特别是非规范和nan处理,我们还没有深⼊研究,这占⽤了⼤量⾯积。但我们可以得出这样的结论:在低位数浮点运算中,乘积成本很低, ⽽累加是昂贵的。
FP32 乘法加法单元
在这⾥,我们提到的所有部分都⾮常明显——将指数相加,尾数的大型乘法器数组,根据需要移动和对齐事物,然后进行归一化吃力(从技术上讲,真正的「融合」乘法加法有点不同,但在这⾥省略了)。
FP8与INT8在⾼效深度学习推理⽅⾯的⽐较(⾼通)
本图表说明了上述所有要点。需要消化的东西很多,但要点是,INT8xINT8累加和累加到定点(FX)的成本是最便宜的,并且是由乘法(mby)主导,⽽使⽤浮点的操作数或累加格式(通常是巨⼤的)主要是累加的成本(alignadd +normacc)。例如,使⽤FP8操作数和「定点」累加器,⽽不是通常的FP32,就可以节省很多成本。
总⽽⾔之,高通论⽂和其他论⽂称,FP8 FMA⽐INT8 FMA多占⽤40-50%的芯⽚⾯积,能耗同样更⾼,甚⾄更糟。这也是⼤多数专⽤ML推理芯⽚使⽤INT8的主要原因。
数字格式设计目标2:准确性
既然整数成本更低,为什么我们不去普遍使⽤INT8和INT16,⽽要⽤FP8和FP16呢?这要看这些格式能在多⼤程度上准确地表示神经⽹络中实际出现的数字。
我们可以把每种数字格式看作⼀个查找表。例如,⼀个2位数字格式可能是这样的:
显然,这组四个数字并没有什么⽤处,因为它缺少了太多数字。事实上,根本就没有负数。如果你的神经⽹络中的某个数字不存在于表格中,那么你能做的就是把它四舍五⼊到最接近的条⽬,这就给神经⽹络带来⼀点误差。
那么,表格中理想的数值集是什么?
比如,如果神经⽹络中的⼤部分数值都接近0(实际情况也是如此),我们就希望能有很多数值接近0,这样我们就能在重要的地⽅获得更⾼的精度,⽽在不重要的地⽅牺牲精度。
在实践中,神经⽹络通常是正态分布或拉普拉斯分布(laplace distributed),有时会出现⼤量离群值,这取决于模型结构的具体数值。特别是在超⼤语⾔模型中,往往会出现极端离群值,这些 离群值虽然罕见,但对模型的功能⾮常重要。
上图显⽰了LLAMA-65B部分的权重,这看起来很像正态分布。如果将其与FP8和INT8中数字的分布进⾏⽐较,就会发现浮点运算的重点⾮常明显——接近于0。这就是我们使⽤浮点运算的原因!
不过,它与真实分布的匹配度仍然不⾼,每次指数递增时都会出现尖锐点,但⽐int8好得多。
我们能做得更好吗?从0开始设计格式的⼀种⽅法是尽量减少平均绝对误差,即四舍五⼊造成的平均损失。
对数系统
例如,英伟达在HotChips⼤会上提出对数系统是继续扩展8位数字格式的可能途径。
要知道,对数系统的四舍五⼊误差⼀般较⼩,但也存在⼀些问题,包括加法器的成本⾼得惊⼈。
NF4及其变体(AF4)是⼀种4位格式,使⽤精确查找表来最⼩化误差,假定权重遵循完全正态分布。但这种⽅法在⾯积和功耗上都⾮常高昂——现在每次操作都需要查找⼀个庞⼤的条⽬表,这⽐任何INT/FP操作都要糟糕得多。
⽬前有许多替代格式:posits、ELMA、PAL等。这些格式声称在计算效率或表述准确性⽅⾯有各种优势,但都还没有达到商业相关的规模。
也许其中的⼀种,或者⼀种尚未发表/发现的,将具有INT的成本和FP的表征准确性——目前有⼏种已经提出了这⼀主 张,甚⾄更好。
这篇文章的作者对Lemurian Labs PAL抱有很⼤希望,但他们的数字格式还有很多未披露之处。他们声称⾃⼰的16位精度和范围都优于FP16和BF16,同时硬件成本也更低。
随着不断扩展8位格式,PAL4还声称其分布⽐英伟达在HotChips上提出的对数系统更好。他们的论文声明令⼈惊叹,但⽬前还没有硬件实现这种格式......。
区块数字格式
⼀个有趣的现象是,张量中的元素⼏乎总是与附近的元素⼤⼩相似。当张量中的元素⽐通常情况下⼤很多时,附近的元素基本上就不重要了——它们相对来说太⼩,无法在点积中看到。
我们可以利⽤这⼀点——可以在多个元素之间共享⼀个指数,⽽不是在每个数字上都有⼀个浮点指数。这样可以节省⼤量冗余指数。
这种⽅法已经存在了⼀段时间——Nervana Flexpoint、微软MSFP12、英伟达VSQ,以及2023年OCP推出的Microscaling。
在这⼀点上,存在着⼀整套不同权衡的可能格式。微软曾试图量化硬件的设计空间:
硬件供应商⾯临着⼀个棘⼿的问题,即既要设计⾼度专业化的⾼效格式,又要不影响未来模型架构的发展,因为未来的模型架构可能会有截然不同的数值分布。
推理
推理过程对成本和功耗特别敏感,因为一个模型虽然只训练一次,却要服务于数以百万计的用户。
因此,推理用的芯片会更倾向于采用更经济、体积更小的数值格式。而这很可能会导致,模型在训练时使用的格式与推理中使用的差异巨大。
目前,市面上有很多工具可以实现格式的转换。
在方法谱系的一端,训练后量化(Post-Training Quantization, PTQ)可以仅通过一些简单的算法来更新模型的权重,而无需执行任何实际的训练步骤:
- 最基本的方法是直接将每个权重值四舍五入到最接近的数值
- LLM.int8()将大部分权重,除了一小部分异常值,转换成INT8格式
- GPTQ利用权重矩阵的二阶信息来实现更精细的量化处理
- Smoothquant采用一种数学上等价的变换方法,来减少异常的激活值
- AWQ根据激活值的数据来更精确地量化最关键的权重
- QuIP对模型的权重进行预处理,降低其对量化过程的敏感性
- AdaRound将每一层的权重四舍五入的过程视为一个二次二元优化问题,进行独立优化
然而,这种方法虽然极大地减少了成本,但实际带来的性能损失要比宣称的大得多。
在另一端,量化感知训练(Quantization-Aware Training, QAT)通过调整模型的精度,并继续训练一段时间来适应新的精度。
这种方式直会接利用常规的训练流程让模型适应量化后的状态,效果更好但相应的计算成本也更高。
训练
因为涉及到反向传播,训练过程相对更复杂。
整个过程中包括了三次矩阵乘法操作:一次发生在前向传播,另外两次发生在反向传播中。
在每个训练步骤中,系统会接收当前的权重值,然后通过与不同数据进行一系列矩阵乘法计算,最终产出更新后的权重值。
FP8格式的训练流程则更加复杂。下面英伟达提出的FP8训练流程的一个简化版:
- 过程中的每次矩阵乘法计算都以FP8 x FP8格式进行,并将结果累积到更高精度的FP32中。之后,为了进行下一层的计算,这个结果会被量化回FP8格式。之所以需要更高精度来进行累积,是因为它包含了成千上万次的小幅度更新,这些微小的变化需要足够的精度才能确保不会被忽略掉。
- 每个FP8格式的权重张量都有一个比例因子。鉴于每一层网络的数据范围可能截然不同,调整数据来适应每一层的特定范围非常关键。
- 在主要计算流程之外,权重更新对精度的要求也是极高的,通常需要保持在如FP32这样更高的精度水平。这是因为权重的微小更新与原有权重值相比,数量级差异巨大,因此需要足够的精度来确保这些小的更新不会因为四舍五入而消失不见。
最后,训练和推理的一个显著区别在于,训练过程中的梯度值会出现更加极端的异常点,这一点非常关键。
虽然可以将激活函数的梯度量化为INT8格式(例如使用SwitchBack或AQT技术),但权重梯度至今仍难以进行这样的量化,因此它必须保持在FP16或者是特殊格式的 FP8(1,5,2)中。
硬件厂商
在量化技术这一领域,无论是HuggingFace的模型量化工具,还是硬件供应商们,都在为了实现更低的比特数、更高的准确率和更好的能效而不懈努力。
然而,这个问题远不止比特数那么简单——硬件中蕴含着极大的复杂性,涉及到多种不同的格式,而这些都有待进一步的优化。
为了跟上黄氏定律(Huang"s Law),硬件供应商们也正在积极响应这一挑战。
首先,Lemurian Labs正专注于开发他们自有的独特数字格式。另一家初创公司MatX则将int4数据类型作为他们的核心目标。这两家公司的方向与其他供应商大相径庭。当然,谷歌也在开辟自己的道路。
至于英伟达、AMD、英特尔、微软、Meta、Arm和高通,则都在聚焦于Microscaling(MX)格式的开发。
然而,即便存在一个共同的标准,也有许多可调整的参数——不仅块大小可以根据需要配置,数据类型的选择也同样灵活。
得益于8位指数的块级编码,微缩(microscaling)格式比传统的FP16浮点格式能表示更宽的数值范围。
即便是精度最高、数值范围最小的MXINT8,其表示范围也超过了FP16,而且在32或64位块大小的情况下,所需的数据位数大约只有FP16的一半。
有趣的是,微软虽然是这些格式的研究和标准化工作的领头羊,却没有选择支持MXINT8。据了解,他们在Braga只支持MXFP4、FXFP6和MXFP8这几种格式。
Meta计划在他们与Andes共同设计的CPU核心中支持微缩格式,这些核心将应用于他们自研的加速器中。AMD和英伟达也在全力以赴地支持这些新格式,并将其应用于下一代GPU中。
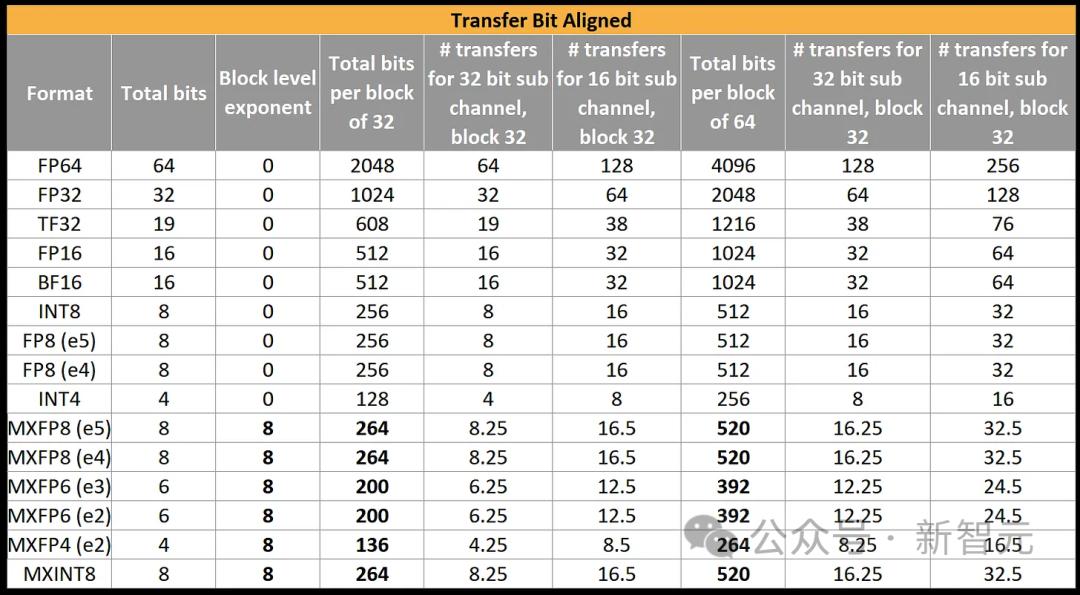
位对齐是一个关键点。DRAM是通过通道来传输数据的。
在DDR和HBM中,最小的子通道数据传输单位是32位,而在LPDDR中,这个单位是16位。这就导致了OCP微缩放格式在数据传输时会出现不常见的大小。
对于FP16和BF16,它们通过16、32或64位的子通道来传输数据,并以此来读取或写入32或64个数值。
然而,当DRAM按16或32位的增量进行数据传输,而需要传输32或64个微缩格式数值的数据块时,就必须传输相当于数据块指数的四分之一或一半。
这意味着,要么损失部分理论内存带宽,要么就必须以128为一组进行传输。编译器和底层程序员在直接为各种加速器编程时,需要考虑这一点。
相比之下,谷歌决定不遵循这一标准,而是为其未来的TPU开拓自己的发展道路。
参考资料:
https://www.semianalysis.com/p/neural-network-quantization-and-number
为了应对大模型不断复杂的推理和训练,英伟达、AMD、英特尔、谷歌、微软、Meta、Arm、高通、MatX以及Lemurian Labs,纷纷开始研发全新的硬件解决方案。
从32位,到16位,再到8位,量化在加速神经⽹络⽅⾯发挥了巨⼤作⽤。
放眼一看,世界把所有的⽬光都聚焦在数字格式上。因为在过去的⼗年中,AI硬件效率的提⾼有很⼤⼀部分要归功于数字格式。
较低精度的数字格式,帮助推倒了数十亿参数模型的内存墙。
英伟达声称,过去10年,单芯⽚TOPS提升了足足1000倍,英伟达自身就加起来达16倍。相⽐之下,从28nm到5nm,⼯艺技术的改进仅为2.5倍!
Semianalysis的最新文章中,从数字格式的基本原理出发,深⼊探讨了神经⽹络量化的技术现状。
本⽂中,将介绍浮点与整数、电路设计注意事项、块浮点、MSFP、微缩格式、对数系统等内容,还会介绍量化和推理数字格式的差异,以及⾼精度与低精度训练方法。
此外,鉴于量化和精度损失带来的挑战,稳重还将讨论模型的下⼀步发展。
最后,文中将介绍英伟达、AMD、英特尔、谷歌、微软、Meta、Arm、高通、 MatX和Lemurian Labs等硬件开发商在扩展⽬前流⾏的8位格式(如FP8和Int8) 时将采⽤的技术。
矩阵乘法
任何现代机器学习模型的主体都是矩阵乘法。
在GPT-3中,每⼀层都要进⾏⼤量的矩阵乘法运算:例如,其中⼀个具体运算是⼀个(2048 x 12288)矩阵乘以⼀个(12288 x 49152)矩阵,然后输出⼀个(2048 x 49152)矩阵。
重要的是如何计算输出矩阵中的每个元素,这可以归结为两个⾮常⼤的向量的点积(在上⾯的例⼦中,⼤⼩为12288)。
这包括12288次乘法和12277次加法,累积成⼀个数字,即输出矩阵的单个元素。
通常情况下,通过硬件将累加器寄存器初始化为0,然后反复:
- 乘以 x_i * w_i
- 将其加⼊累加器
每个周期的吞吐量均为1,经过~12288个周期后,输出矩阵的单个元素的累加完成。
这种「融合乘加」运算(FMA)是机器学习的基本计算单元:芯⽚上成千上万个FMA单元经过策略性排列,可⾼效地重复使⽤数据,从⽽并⾏计算输出矩阵的许多元素,从而减少所需的周期数。
上图中的所有数字都需要以某种⽅式,在芯⽚内的某个位置⽤位表示:
- x_i,输⼊激活
- w_i,权重
- p_i,成对乘积
- 在整个输出完成累积之前,所有中间部分累积加和
- 最终输出总和
在这个巨⼤的设计空间中,⽬前⼤多数机器学习量化研究都归结为两个⽬标:
1. 实现良好的能量和⾯积效率。这主要取决于权重和激活所使⽤的数字格式。
2. 既要⾜够精确地存储数千亿个权重,又要使⽤尽可能少的位,以便从容量和带宽的角度减少内存占⽤。这取决于⽤于存储权重的数字格式。
这些⽬标有时是⼀致的,有时是相悖的。接下来文章将对两者进⾏深⼊探讨。
数字格式设计目标1:芯片效率
许多机器学习芯⽚计算性能的根本限制在于功耗。
虽然H100在论文中可以实现2,000 TFLOPS的计算能⼒,但在此之前就会遇到功耗限制,因此每焦⽿能量的FLOPs是⼀个极其重要的跟踪指标。
鉴于现在的训练运⾏经常超过1e25 FLOP,我们需要极其⾼效的芯⽚,在数⽉内消耗兆⽡级的电⼒,以击败SOTA。
基本数字格式
首先深入了解计算中最基本的数字格式:整数。
基数为2正整数
正整数可以用2进制(基数为2)来自然表示。这种表示法称为UINT,即⽆符号整数。下⾯是⼀些8位⽆符号整数的例⼦,也称为UINT8,从0到255。
这些整数的位数不限,但通常只⽀持以下四种格式:UINT8、UINT16、UINT32和UINT64。
负整数
负整数需要⼀个符号来区分正负,只需在最显著位加上⼀个符号即可:例如, 0011表示+3,1011表示-3。这称为符号-数值表示。
下⾯是INT8的⼀些示例,INT8从-128到127。请注意,由于第⼀位是符号,最⼤值实际上减半了,从255到127。
符号大小是直观的,但效率很低——你的电路必须实现相当不同的加法和减法算法,⽽这些算法又与⽆符号整数的电路不同。
有趣的是,硬件设计⼈员可以通过使⽤⼆进制表示法来解决这个问题,这样就可以对正数、负数和⽆符号数使⽤完全相同的进位阶梯电路。所有现代CPU都使⽤⼆进制表⽰法。
在⽆符号int8中,255的最⼤值是1111111111。在有符号int8中,最⼩值为-128,最⼤值为127。
为了让INT8和UINT8共享硬件资源,可以⽤1111111111来表⽰-1。现在,当数字1相加时,会溢出到00000000,如预期的那样表示0。同样,11111110也可以表⽰为-2。
溢出是一种特征!实际上,0到127被映射为正常值,128到255被直接映射到-128到-1。
定点数
更进⼀步说,我们可以在现有硬件上轻松制作新的数字格式,⽆需修改。
虽然这些都是整数,但你也可以想象它们是其他数的倍数!例如,0.025就是千分之25,可以直接存储为整数25。现在,我们只需在其他地⽅记住所有正在使⽤的数字都是千分之⼀。
新的「数字格式」可以⽤千分之⼀来表示-0.128到0.127的数字,实际逻辑没有变化。整数仍被视为整数,然后⼩数点被固定在右起第三个位置。这种策略称为定点法。
⼀般来说,这是⼀个有⽤的策略,本⽂中会经常提到——如果你想改变可以表示的数字范围,可以在某个地⽅添加⼀个⽐例因⼦。(很明显,你可以在⼆进制中这样做,但⼗进制更容易讨论)。
浮点数
不过,定点也有⼀些缺点,尤其是乘法运算。⽐⽅说,你需要计算1万亿乘以1万亿分之⼀。
⼤⼩上的巨⼤差异就是⾼「动态范围」的⼀个例⼦。那么10^12和10^-12都必须⽤数字格式来表示,因此很容易计算出需要多少位:从0到1万亿,以1万亿为增量,需要10^24的增量,log2(10^24)~= 80 位,才能以我们想要的精度表示动态范围。
每个数字是80位显然是非常浪费的。你不⼀定关⼼绝对精度,你需要关⼼的是相对精度。
因此,即使上述格式能够准确区分1万亿和999,999,999,999.9999999999之间的误差(⼀般也不需要区分)。⼤多数情况下,你关⼼的是相对于数字⼤⼩的误差量。
这正是科学记数法所要解决的问题:在前⾯的例⼦中,我们可以将⼀万亿写成1.00 * 10^12,将⼀万亿分之⼀写成 1.00 * 10^-12,这样存储量就⼩得多了。
这样虽然更复杂,但可以让你在相同的上下⽂中毫⽆顾虑地表示极⼤和极⼩的数字。
因此,除了符号和数值外,我们现在还有⼀个指数。IEEE 754-1985在当时使⽤的许多略有不同的⼆进制格式中,标准化了业界通⽤的⼆进制存储⽅式。
主要的有趣格式——32位浮点数(float32或FP32)可以描述为 (1,8,23):1个符号位、8个指数位和23个尾数位。
- 符号位为0表⽰正,1表示为负。
- 指数位被解释为⽆符号整数e,代表⽐例因⼦2^e-127,其价值介于2^-126和2^127。更多的指数位意味着更⼤的动态范围。
- 尾数位代表数值1。更多的尾数位意味着更⾼的相对精度。
其他位宽已被标准化或显示采⽤,例如FP16(1,5,10)和BF16(1,8,7)。而争论的焦点在于范围与精度。
FP8(1,5,2或1,4,3)最近在OCP标准中标准化了一些额外的奇怪规定,但目前还没有定论。许多人工智能硬件公司已经实现了具有稍微优越的变体的芯片,但这些变体与标准不兼容。
芯片效率
说回硬件效率,所使⽤的数字格式对所需的芯⽚⾯积和功耗有巨⼤影响。
整数芯片电路设计
整数加法器是有史以来研究得最透彻的芯片设计问题。
虽然加法器的实际实现要复杂得多,但有⼀种⽅法可以让我们把加法器想象成⼀路加法并根据需要携带1,因此从某种意义上说,⼀个n位加法器所做的⼯作量与n成正⽐。
关于乘法,回想⼀下⼩学的长乘法。我们进⾏n位数乘以1位数的乘积,最后将所有结果相加。
在⼆进制中,乘以⼀位数是微不⾜道的(0或1)。这意味着n位乘法器实质上是n位加法器的n次重复,因此⼯作量与n^2成正⽐。
虽然实际应⽤因⾯积、功耗和频率限制⽽⼤不相同,但⼀般来说:1)乘法器⽐加法器昂贵得多;2)在低位数(8位及以下)情况下,FMA的功耗和⾯积成本相对于加法器的贡献越来越⼤(n对n^2缩放)。
浮点电路
浮点运算单位则⼤不相同。相⽐之下,乘积/乘法相对简单。
- 如果输⼊的符号中正好有⼀个是负号,则符号为负,否则为正。
- 指数是输⼊指数的整数和。
- 尾数是输⼊尾数的整数乘积。
相⽐之下,总和相当复杂。
- ⾸先,求指数的差值。(假设exp1⾄少和exp2⼀样⼤,如果不⼀样⼤,则在指令中进⾏交换)
- 将尾数2向下移动(exp1-exp2),使其与尾数1对齐。
- 在每个尾数中加⼊⼀个隐含的前导1。如果⼀个符号是负数,则对其中⼀个尾数进⾏2的补码运算。
- 将尾数相加形成输出尾数。
- 如果出现溢出,则将结果指数增加1,并将尾数向下移动。
- 如果结果为负数,则将其转换回⽆符号尾数,并将输出符号设为负数。
- 对尾数进⾏归⼀化处理,使其具有前导1,然后删去隐式前导1。
- 对尾数进⾏适当的四舍五⼊(通常是四舍五⼊到最近的偶数)。
值得注意的是,浮点乘法甚⾄可以⽐整数乘法成本更少,因为尾数乘积中的位数更少,⽽指数的加法器⽐乘法器⼩得多,⼏乎没有关系。
显然,这也是经过极度简化的,特别是非规范和nan处理,我们还没有深⼊研究,这占⽤了⼤量⾯积。但我们可以得出这样的结论:在低位数浮点运算中,乘积成本很低, ⽽累加是昂贵的。
FP32 乘法加法单元
在这⾥,我们提到的所有部分都⾮常明显——将指数相加,尾数的大型乘法器数组,根据需要移动和对齐事物,然后进行归一化吃力(从技术上讲,真正的「融合」乘法加法有点不同,但在这⾥省略了)。
FP8与INT8在⾼效深度学习推理⽅⾯的⽐较(⾼通)
本图表说明了上述所有要点。需要消化的东西很多,但要点是,INT8xINT8累加和累加到定点(FX)的成本是最便宜的,并且是由乘法(mby)主导,⽽使⽤浮点的操作数或累加格式(通常是巨⼤的)主要是累加的成本(alignadd +normacc)。例如,使⽤FP8操作数和「定点」累加器,⽽不是通常的FP32,就可以节省很多成本。
总⽽⾔之,高通论⽂和其他论⽂称,FP8 FMA⽐INT8 FMA多占⽤40-50%的芯⽚⾯积,能耗同样更⾼,甚⾄更糟。这也是⼤多数专⽤ML推理芯⽚使⽤INT8的主要原因。
数字格式设计目标2:准确性
既然整数成本更低,为什么我们不去普遍使⽤INT8和INT16,⽽要⽤FP8和FP16呢?这要看这些格式能在多⼤程度上准确地表示神经⽹络中实际出现的数字。
我们可以把每种数字格式看作⼀个查找表。例如,⼀个2位数字格式可能是这样的:
显然,这组四个数字并没有什么⽤处,因为它缺少了太多数字。事实上,根本就没有负数。如果你的神经⽹络中的某个数字不存在于表格中,那么你能做的就是把它四舍五⼊到最接近的条⽬,这就给神经⽹络带来⼀点误差。
那么,表格中理想的数值集是什么?
比如,如果神经⽹络中的⼤部分数值都接近0(实际情况也是如此),我们就希望能有很多数值接近0,这样我们就能在重要的地⽅获得更⾼的精度,⽽在不重要的地⽅牺牲精度。
在实践中,神经⽹络通常是正态分布或拉普拉斯分布(laplace distributed),有时会出现⼤量离群值,这取决于模型结构的具体数值。特别是在超⼤语⾔模型中,往往会出现极端离群值,这些 离群值虽然罕见,但对模型的功能⾮常重要。
上图显⽰了LLAMA-65B部分的权重,这看起来很像正态分布。如果将其与FP8和INT8中数字的分布进⾏⽐较,就会发现浮点运算的重点⾮常明显——接近于0。这就是我们使⽤浮点运算的原因!
不过,它与真实分布的匹配度仍然不⾼,每次指数递增时都会出现尖锐点,但⽐int8好得多。
我们能做得更好吗?从0开始设计格式的⼀种⽅法是尽量减少平均绝对误差,即四舍五⼊造成的平均损失。
对数系统
例如,英伟达在HotChips⼤会上提出对数系统是继续扩展8位数字格式的可能途径。
要知道,对数系统的四舍五⼊误差⼀般较⼩,但也存在⼀些问题,包括加法器的成本⾼得惊⼈。
NF4及其变体(AF4)是⼀种4位格式,使⽤精确查找表来最⼩化误差,假定权重遵循完全正态分布。但这种⽅法在⾯积和功耗上都⾮常高昂——现在每次操作都需要查找⼀个庞⼤的条⽬表,这⽐任何INT/FP操作都要糟糕得多。
⽬前有许多替代格式:posits、ELMA、PAL等。这些格式声称在计算效率或表述准确性⽅⾯有各种优势,但都还没有达到商业相关的规模。
也许其中的⼀种,或者⼀种尚未发表/发现的,将具有INT的成本和FP的表征准确性——目前有⼏种已经提出了这⼀主 张,甚⾄更好。
这篇文章的作者对Lemurian Labs PAL抱有很⼤希望,但他们的数字格式还有很多未披露之处。他们声称⾃⼰的16位精度和范围都优于FP16和BF16,同时硬件成本也更低。
随着不断扩展8位格式,PAL4还声称其分布⽐英伟达在HotChips上提出的对数系统更好。他们的论文声明令⼈惊叹,但⽬前还没有硬件实现这种格式......。
区块数字格式
⼀个有趣的现象是,张量中的元素⼏乎总是与附近的元素⼤⼩相似。当张量中的元素⽐通常情况下⼤很多时,附近的元素基本上就不重要了——它们相对来说太⼩,无法在点积中看到。
我们可以利⽤这⼀点——可以在多个元素之间共享⼀个指数,⽽不是在每个数字上都有⼀个浮点指数。这样可以节省⼤量冗余指数。
这种⽅法已经存在了⼀段时间——Nervana Flexpoint、微软MSFP12、英伟达VSQ,以及2023年OCP推出的Microscaling。
在这⼀点上,存在着⼀整套不同权衡的可能格式。微软曾试图量化硬件的设计空间:
硬件供应商⾯临着⼀个棘⼿的问题,即既要设计⾼度专业化的⾼效格式,又要不影响未来模型架构的发展,因为未来的模型架构可能会有截然不同的数值分布。
推理
推理过程对成本和功耗特别敏感,因为一个模型虽然只训练一次,却要服务于数以百万计的用户。
因此,推理用的芯片会更倾向于采用更经济、体积更小的数值格式。而这很可能会导致,模型在训练时使用的格式与推理中使用的差异巨大。
目前,市面上有很多工具可以实现格式的转换。
在方法谱系的一端,训练后量化(Post-Training Quantization, PTQ)可以仅通过一些简单的算法来更新模型的权重,而无需执行任何实际的训练步骤:
- 最基本的方法是直接将每个权重值四舍五入到最接近的数值
- LLM.int8()将大部分权重,除了一小部分异常值,转换成INT8格式
- GPTQ利用权重矩阵的二阶信息来实现更精细的量化处理
- Smoothquant采用一种数学上等价的变换方法,来减少异常的激活值
- AWQ根据激活值的数据来更精确地量化最关键的权重
- QuIP对模型的权重进行预处理,降低其对量化过程的敏感性
- AdaRound将每一层的权重四舍五入的过程视为一个二次二元优化问题,进行独立优化
然而,这种方法虽然极大地减少了成本,但实际带来的性能损失要比宣称的大得多。
在另一端,量化感知训练(Quantization-Aware Training, QAT)通过调整模型的精度,并继续训练一段时间来适应新的精度。
这种方式直会接利用常规的训练流程让模型适应量化后的状态,效果更好但相应的计算成本也更高。
训练
因为涉及到反向传播,训练过程相对更复杂。
整个过程中包括了三次矩阵乘法操作:一次发生在前向传播,另外两次发生在反向传播中。
在每个训练步骤中,系统会接收当前的权重值,然后通过与不同数据进行一系列矩阵乘法计算,最终产出更新后的权重值。
FP8格式的训练流程则更加复杂。下面英伟达提出的FP8训练流程的一个简化版:
- 过程中的每次矩阵乘法计算都以FP8 x FP8格式进行,并将结果累积到更高精度的FP32中。之后,为了进行下一层的计算,这个结果会被量化回FP8格式。之所以需要更高精度来进行累积,是因为它包含了成千上万次的小幅度更新,这些微小的变化需要足够的精度才能确保不会被忽略掉。
- 每个FP8格式的权重张量都有一个比例因子。鉴于每一层网络的数据范围可能截然不同,调整数据来适应每一层的特定范围非常关键。
- 在主要计算流程之外,权重更新对精度的要求也是极高的,通常需要保持在如FP32这样更高的精度水平。这是因为权重的微小更新与原有权重值相比,数量级差异巨大,因此需要足够的精度来确保这些小的更新不会因为四舍五入而消失不见。
最后,训练和推理的一个显著区别在于,训练过程中的梯度值会出现更加极端的异常点,这一点非常关键。
虽然可以将激活函数的梯度量化为INT8格式(例如使用SwitchBack或AQT技术),但权重梯度至今仍难以进行这样的量化,因此它必须保持在FP16或者是特殊格式的 FP8(1,5,2)中。
硬件厂商
在量化技术这一领域,无论是HuggingFace的模型量化工具,还是硬件供应商们,都在为了实现更低的比特数、更高的准确率和更好的能效而不懈努力。
然而,这个问题远不止比特数那么简单——硬件中蕴含着极大的复杂性,涉及到多种不同的格式,而这些都有待进一步的优化。
为了跟上黄氏定律(Huang"s Law),硬件供应商们也正在积极响应这一挑战。
首先,Lemurian Labs正专注于开发他们自有的独特数字格式。另一家初创公司MatX则将int4数据类型作为他们的核心目标。这两家公司的方向与其他供应商大相径庭。当然,谷歌也在开辟自己的道路。
至于英伟达、AMD、英特尔、微软、Meta、Arm和高通,则都在聚焦于Microscaling(MX)格式的开发。
然而,即便存在一个共同的标准,也有许多可调整的参数——不仅块大小可以根据需要配置,数据类型的选择也同样灵活。
得益于8位指数的块级编码,微缩(microscaling)格式比传统的FP16浮点格式能表示更宽的数值范围。
即便是精度最高、数值范围最小的MXINT8,其表示范围也超过了FP16,而且在32或64位块大小的情况下,所需的数据位数大约只有FP16的一半。
有趣的是,微软虽然是这些格式的研究和标准化工作的领头羊,却没有选择支持MXINT8。据了解,他们在Braga只支持MXFP4、FXFP6和MXFP8这几种格式。
Meta计划在他们与Andes共同设计的CPU核心中支持微缩格式,这些核心将应用于他们自研的加速器中。AMD和英伟达也在全力以赴地支持这些新格式,并将其应用于下一代GPU中。
位对齐是一个关键点。DRAM是通过通道来传输数据的。
在DDR和HBM中,最小的子通道数据传输单位是32位,而在LPDDR中,这个单位是16位。这就导致了OCP微缩放格式在数据传输时会出现不常见的大小。
对于FP16和BF16,它们通过16、32或64位的子通道来传输数据,并以此来读取或写入32或64个数值。
然而,当DRAM按16或32位的增量进行数据传输,而需要传输32或64个微缩格式数值的数据块时,就必须传输相当于数据块指数的四分之一或一半。
这意味着,要么损失部分理论内存带宽,要么就必须以128为一组进行传输。编译器和底层程序员在直接为各种加速器编程时,需要考虑这一点。
相比之下,谷歌决定不遵循这一标准,而是为其未来的TPU开拓自己的发展道路。
参考资料:
https://www.semianalysis.com/p/neural-network-quantization-and-number
版权声明
本文收集整理自网络,如有侵权,请联系删除。